Punto
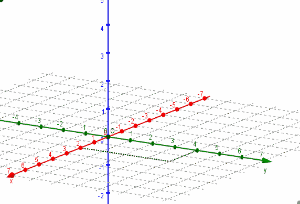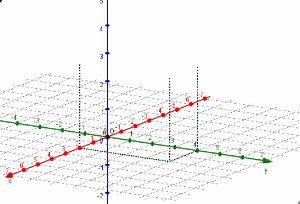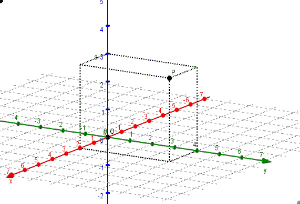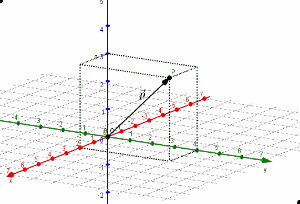
En los sistemas de representación, los puntos se designan con una letra mayúscula (A, B, C…), y su posición se marca con una pequeña cruz, círculo, cuadrado o triángulo.
Si se considera un sistema cartesiano plano de coordenadas, el punto tendrá en él dos coordenadas x e y. Si se está representando en un sistema espacial, se tomarán en cuenta tres coordenadas (x, y, z).
La posición de un punto también puede definirse mediante sistemas de coordenadas diferentes, como, entre otros, el de coordenadas polares, el de esféricas o el de cilíndricas.
UCA. (2017). El Punto. Septiembre 13, 2019, de UCA Sitio web: http://dibujoindustrial.es/geomplana/geometriabasica/el-punto/
http://dibujoindustrial.es/geomplana/geometriabasica/el-punto/
Línea
Una recta es una sucesión ininterrumpida de puntos con una misma dirección, por lo tanto sólo tiene una dimensión. Dos puntos determinan una recta la recta es infinita, no posee ni principio ni fin.- Recta: La recta propiamente dicha se caracteriza porque los puntos que la forman están en la misma dirección. Tiene una sola dirección y dos sentidos. No se puede medir.
- Semirrecta: Es línea recta que tiene origen pero no tiene fin, tiene sólo un sentido, y no se puede medir.

- Segmento: Un segmento es una línea recta que tiene principio y fin, un segmento se puede medir.
- Poligonal: Se llama recta poligonal aquella que está formada por varias porciones de rectas que están unas a continuación de otras, pero no están alineadas, la línea poligonal puede ser abierta (cuando ningún extremo se une) o cerrada (cuando el primer extremo se une con el último). La línea poligonal cerrada forma una figura plana que se llama polígono.

- Curva: Una curva está formada por puntos que están en distinta dirección. Puede ser curva abierta (los externos no se unen) curva cerrada (cuyos extremos se unen) y curva mixta (formada por lineas rectas y curvas unidas)

estudiantes. (2015). Matemáticas: Puntos y rectas. Septiembre 13, 2019, de tuespaciojoven Sitio web: http://www.estudiantes.info/matematicas/1eso/images/puntos-y-rectas-desarrollo.htm
Planos
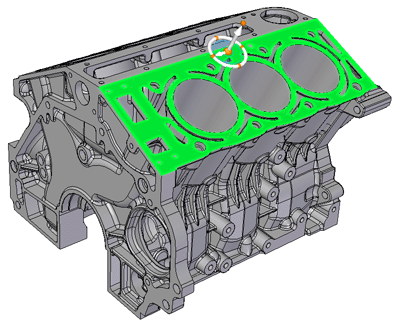
Los planos son la superficie que es generada por la intersección de una o más líneas rectas o curvas, pueden ser cuadrada, rectangular, circular, triangular, irregular, etc.- Plano paralelo al Plano Vertical (PV): está en verdadera magnitud en su proyección de vertical, mientras que las proyecciones horizontal y de perfil, son una recta de las dimensiones del tamaño del plano.

- Plano paralelo al Plano Horizontal (PH): En este caso, el plano se ve en verdadera magnitud en la proyección horizontal, mientras que las proyecciones vertical y de perfil, son una recta.
- Plano paralelo al Plano de Perfil (PP): De forma análoga a los casos anteriores, tenemos la verdadera magnitud en la proyección de perfil. Las otras dos proyecciones, son rectas.
Dibujo tecnico. (2018). Proyección de planos. Planos paralelos. Septiembre 13, 2019, de wordpress Sitio web: https://ibiguridt.wordpress.com/temas/sistemas-de-representacion/proyeccion/
Paralelismo
Definición y trazados Rectas paralelas son aquellas que, estando en un mismo plano, no se cortan en un espacio finito, o se cortan en el infinito.- Paralelismo entre rectas: Dos rectas son paralelas cuando sus proyecciones correspondientes son paralelas.

- Paralelismo entre recta y plano: Un plano es paralelo a una recta cuando contiene una recta paralela a la primera. También podemos decir que un plano es paralelo a una recta si existe otro plano paralelo al primero que contenga a la recta.
- Paralelismo entre planos: Dos planos son paralelos si sus trazas son paralelas.
- Paralelismo entre planos: Dos planos son paralelos si sus trazas son paralelas.
Mena, M.. (2012). Paralelismo y Perpendicularidad. Septiembre 13, 2019, de sites.google Sitio web: https://sites.google.com/site/dibujotecnicoclm/u/sistema-diedrico/paralelismo-y-perpendicularidad
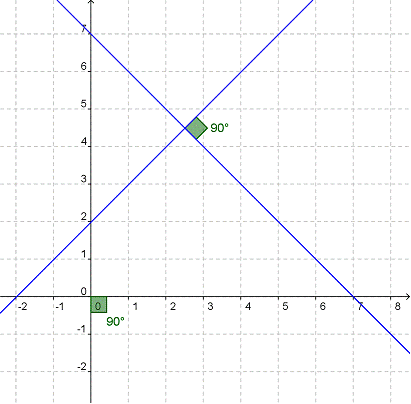
Perpendiculares
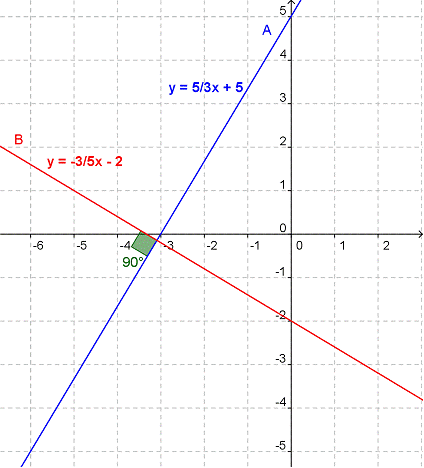
Las líneas perpendiculares son dos o más líneas que se intersectan con un ángulo de 90 grados, como las dos líneas en ésta gráfica, y los ejes x y y que las orientan.
montereyinstitute. (2014). Líneas Perpendiculares. Septiembre 13, 2019, de montereyinstitute Sitio web: https://www.montereyinstitute.org/courses/Algebra1/COURSE_TEXT_RESOURCE/U04_L2_T2_text_final_es.html
https://www.montereyinstitute.org/courses/Algebra1/COURSE_TEXT_RESOURCE/U04_L2_T2_text_final_es.html